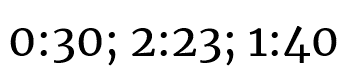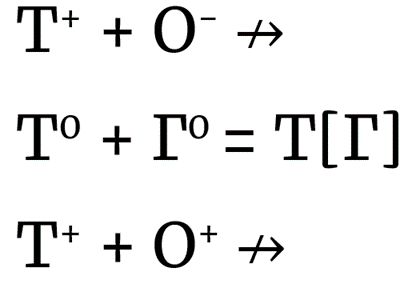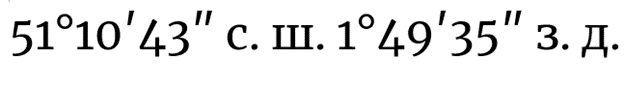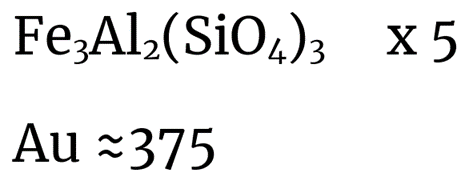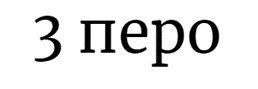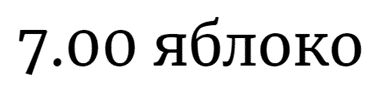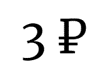Как прошёл весенний сезон учебно-тренировочных чемпионатов Центра педагогического мастерства в 2023 году?
Чтобы вам было удобнее, мы создали навигацию по новости! Используйте кнопки и переходите в интересующий вас раздел.
Материал подготовил Роман Илюшин, руководитель учебной части отдела развития таланта школьников Центра педагогического мастерства.
Что такое учебно-тренировочные чемпионаты?
Учебно-тренировочные чемпионаты (УТЧ) — это большие межпредметные интеллектуальные соревнования, которые проходят в онлайн- и офлайн-форматах в несколько этапов.
Кто может участвовать в УТЧ?
Ученики 7–11 классов школ и колледжей, интересующиеся олимпиадами по общеобразовательным предметам, а также исследовательской и проектной деятельностью.
В чем особенность формата чемпионатов?
Соревнования отличаются как от диагностических работ и государственных экзаменов по школьной программе, так и от Всероссийской или перечневых олимпиад школьников:
- во-первых, все чемпионаты являются командными состязаниями, поэтому помимо развития hard-skills, предметных навыков, УТЧ требует от участников серьезных гибких навыков: коммуникативных, творческих, организационных;
- во-вторых, соревнования не приносят образовательным организациям баллов в рейтинг: только наиболее мотивированные школы и наиболее мотивированные ученики, которые ищут новые форматы подготовки к олимпиадам, новые форматы интеллектуальных соревнований, принимают участие в УТЧ;
- в-третьих, УТЧ — это межпредметные соревнования: даже лингвистическое соревнование МЫШ — о котором ниже — требует эрудированности в области математики, информатики, истории, литературы и искусства.

Зачем участвовать в УТЧ?
Школьники участвуют в чемпионатах по разным причинам. Мы провели несколько небольших исследований, и вот что нам рассказали участники УТЧ: они участвуют, потому что ожидают, что в наших соревнованиях будет что-то интересное, свежее и необычное, будут очень интересные, но в тот же момент и сложные задания, а не «сухонаучные» вопросы. Школьники приходят на чемпионаты ради бодрейшей атмосферы, эмоций, которых не передать словами. Участники говорят, что в УТЧ они ценят сближение людей и общение. Одна из девятиклассниц так написала о нашем наиболее известном соревновании — КОСМОСе:
Наверное, это единственная олимпиада, в которой я участвую по искреннему желанию.
Призёры и победители УТЧ получают возможность бесплатно поучаствовать в учебно-тренировочных семинарах и выездных школах по любимым предметам от ЦПМ и Ассоциации победителей олимпиад. Кроме того, участники получают фирменный мерч чемпионатов: толстовки, кружки, стикеры, ручки и другие полезные — в том числе для учёбы — вещи.
Какие бывают чемпионаты?
Всего весной прошло три УТЧ: весенний сезон Командного стратегического московского соревнования 2023 года — КОСМОС, VII турнир Московских Ынтеллектуальных Школьников — МЫШ, I Глобального разнообразия интеллектуальный биатлон — ГРИБ.
Командное стратегическое московское соревнование
Первый чемпионат — КОСМОС — проходит с 2019 года и включает в себя задания по подавляющему большинству общеобразовательных предметов:
- математике,
- информатике,
- физике,
- астрономии,
- робототехнике,
- географии,
- экологии,
- биологии,
- химии,
- русскому языку,
- иностранным языкам,
- лингвистике,
- литературе,
- экономике,
- обществознанию,
- праву,
- истории,
- искусству,
- физической культуре,
- ОБЖ.
Командам из 7–15 учащихся 8–11 классов было необходимо пройти сложную миссию, состоящую из пяти соревновательных этапов. Так, по сюжету соревнования искусственный интеллект заставляет землян противостоять космическому нападению и уходить в катакомбы. Участникам необходимо было программировать курсирование космического флота, кодировать и декодировать культурные достижения человечества, разбирать послания предков.

«Моя задача — вписаться в заданные рамки сюжета сезона, дать детям необычный, незаезженный контент, который позволит им удивиться, узнать для себя что-то новое.
Например, для прошедшего КОСМОСа я делал задачу про новгородскую археологию, поскольку она вписывалась в легенду игры практически идеально, а про Новгород дети знают очень мало.
При этом задания не должны быть похожими на стандартные диагностики: ребенок не должен знать или не знать что-то, он должен включить мозг и провести классификацию неизвестных или частично известных ему объектов, объяснить их назначение и вообще как-то поиграться с данной ему информацией.
Я хочу, чтобы в ходе решения подобных заданий дети преодолели шаблонность мышления и научились не бояться нового, поняли, что всё элементарно и что не нужно только заучивать даты, чтобы разбираться в олимпиадной истории», — говорит Николай Домрачев, заведующий кафедрой истории отдела развития таланта школьников (ОРТШ) Центра педагогического мастерства, автор задачи финального этапа КОСМОСа.
Турнир Московских Ынтеллектуальных Школьников
Турнир МЫШ, в названии которого явно можно распознать ошибку, проходит по русскому языку и лингвистике. Чтобы дойти до гранд-финала, командам лингвистов из 5–7 человек 7–11 классов нужно пройти через квалификацию, групповой этап, полуфиналы и три лиги финалов.
Очень лютые задания, организация лучшая, всё понравилось. Варвара, участница VII турнира МЫШ.
Очень интересные задания: они всегда оригинальные, и нужен творческий подход к ним, нужно командой решать — это очень сплочает. Софья, участница VII турнира МЫШ.
ГРИБ
Весной 2023 года турнир прошёл впервые. Это естественно-научное состязание на тему биоразнообразия для команд школьников 8–11 классов в составе 4–7 человек.
Соревнование комплексно освещает мир живой природы через призму экологии, биологии, географии и химии.
Участникам в течение полутора месяцев каждую неделю предлагается решить две комплексных задачи по двум из четырех предметов: это могут быть исследовательские кейсы, сложные многоступенчатые лабораторные работы, проблемные вопросы и объемные тесты.
Всего в соревнованиях приняли участие более 7 000 учеников, из них 4 858 обучающихся — москвичи.
В весеннем сезоне КОСМОСа 2023 года приняли участие 148 команд, в VII турнире МЫШ — 185 команд, в первом ГРИБе — 349 команд.
Кто участвует в УТЧ?
КОСМОС, несмотря на слово московское в названии, имеет очень большую географию: помимо учащихся из столицы, в чемпионате участвуют школьники из Московской области, Республики Мордовии, Чувашской Республики, Брянской области, а также из Узбекистана!
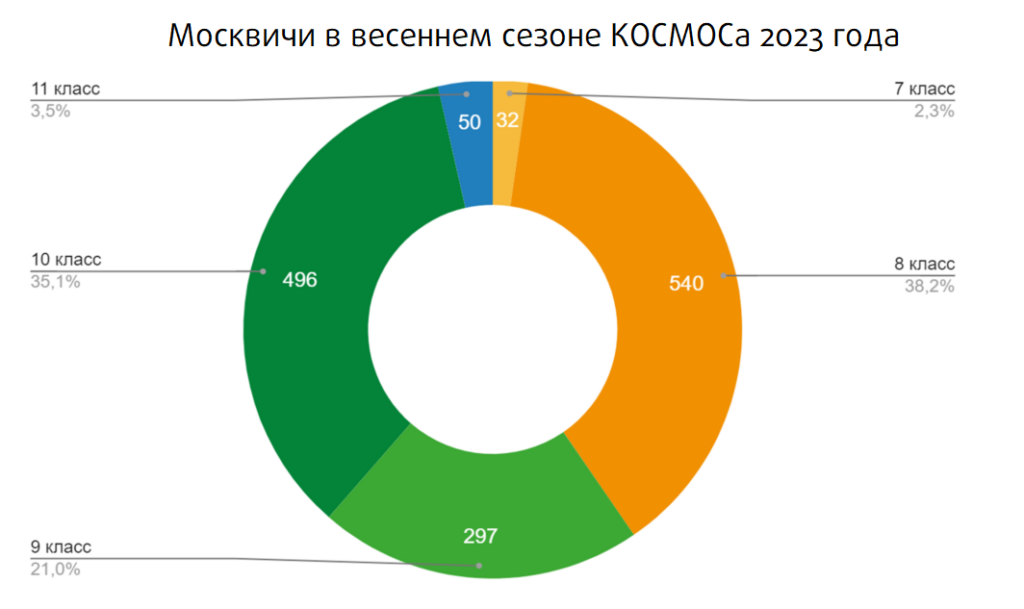
Сколько москвичей приняли участие в соревновании?
В весеннем сезоне КОСМОСа приняли участие обучающиеся из более чем 50 образовательных организаций города Москвы.
Наибольшее количество участников — из ГБОУ «Школа «Дмитровский» имени Героя Советского Союза В.П. Кислякова» в Северном административном округе.
Ниже — список из семи образовательных организаций с наибольшим представительством на турнире.
| Место | Образовательное учреждение | Делегация (чел.) |
| 1. | ГБОУ Школа «Дмитровский» | 84 |
| 2. | ГБОУ Школа № 1095 | 68 |
| 3. | ГБОУ Школа № 2070 | 64 |
| 4. | ГБОУ Школа № 2097 | 60 |
| 5. | ГБОУ Школа № 1596 | 58 |
| 6. | ГБОУ Школа № 1360 | 46 |
| 7. | ГАОУ Школа № 548 | 40 |
Наиболее представленными в соревновании оказались школы из ТиНАО (220 человек), СВАО (193 человека), ЮАО (175 человек) и САО (173 человека).
Лидерские позиции по количеству школ, представленных в соревновании, занимают следующие межрайонные советы директоров (МРСД): № 37 (восемь школ-участниц из ТиНАО), №4 (четыре школы-участницы из районов Алтуфьевский, Бабушкинский, Лосиноостровский, Отрадное и Свиблово) и № 8, 11, 27, 29, 30, 35 (по три школы в соревновании).
Турнир Московских Ынтеллектуальных Школьников (МЫШ) может показаться из-за своего названия несерьезным мероприятием. Кто же участвует в этом соревновании?
Для сравнения: в LII Традиционной олимпиаде по лингвистике, входящей в перечень Минобрнауки РФ и в экосистему Московской олимпиады школьников, в 2021–2022 учебном году приняли участие 3790 человек. Эта олимпиада проводится с 1965 года, абсолютный блокбастер среди олимпиадников-русистов. Сможет ли маленький молодой МЫШ, впервые проведенный на выездной школе в 2018 году тремя преподавателями, сравниться по популярности с почтенной Традиционной олимпиадой?
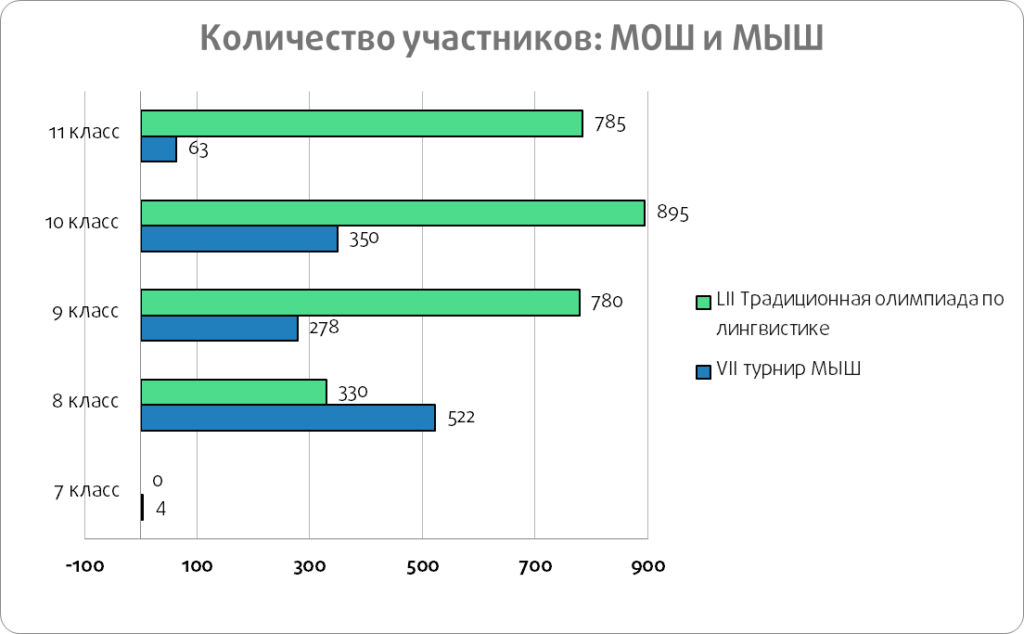
В VII турнире Московских Ынтеллектуальных Школьников, учебно-тренировочном чемпионате по русскому языку и лингвистике от Центра педагогического мастерства, сразились более тысячи учеников.
Можно заметить, что наш чемпионат более популярен среди 7–8 классов: каждый из этапов не занимает больше полутора часов (в отличие от долгих туров МОШ). Семи- и восьмиклассники более охотно участвуют в турнире МЫШ, потому что он интерактивнее и компактнее большой олимпиады.
В VII турнире МЫШ приняли участие обучающиеся из более чем 150 московских школ и образовательных организаций других регионов. Больше всего учеников — 72 человека — направила Школа № 338 города Москвы. Ниже — список из двенадцати организаций с наибольшим представительством на турнире.
| Место | Образовательное учреждение | Делегация (чел.) |
| 1. | ГБОУ Школа № 338 | 72 |
| 2. | ГБПОУ «Колледж полиции» | 60 |
| 3. | ГБОУ Школа № 1517 | 31 |
| 4. | ГБОУ Школа № 1798 «Феникс» | 28 |
| 5. | ГБОУ Школа № 1387 | 27 |
| 6–7. | ГБОУ Школа № 1381 | 25 |
| ГБОУ «Школа в Некрасовке» | 25 | |
| 8. | ГБОУ Школа № 1158 | 23 |
| 9. | ГБОУ Школа № 1317 | 20 |
| 10–12. | ГБОУ Школа № 1434 | 18 |
| ГБОУ Школа № 1223 | 18 | |
| ГБОУ Школа № 1018 | 18 |
Обратимся к географии участников из Москвы.
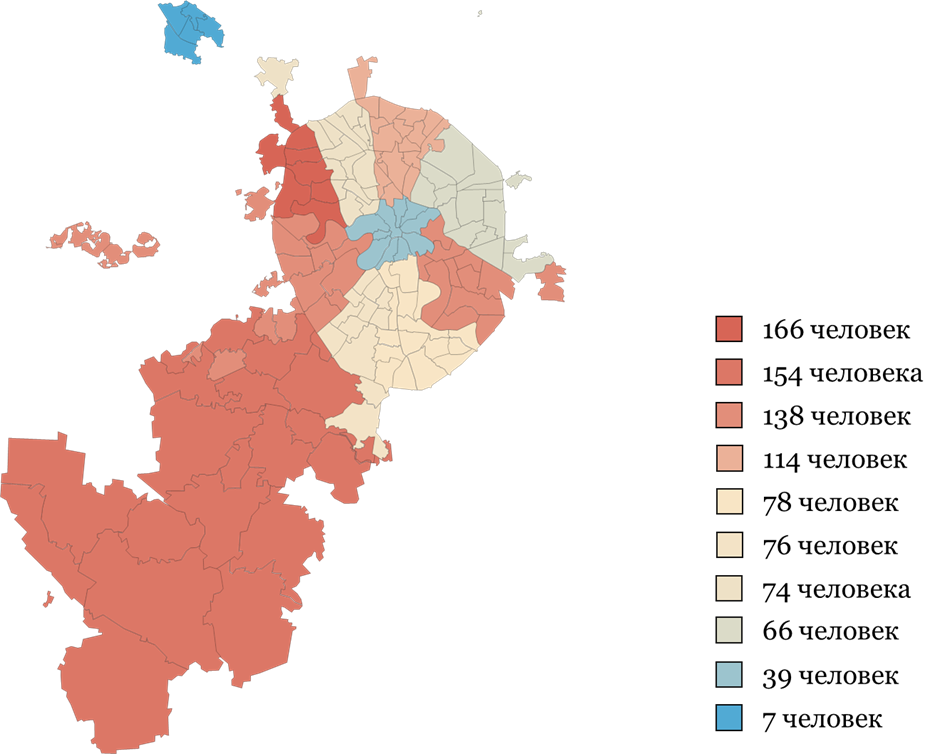
Больше всего учеников — из СЗАО (166 человек) и ТиНАО (154 ученика).
Замыкают список округов-лидеров ЮВАО и ЗАО (по 138 обучающихся).
В первом Глобального разнообразия интеллектуальном биатлоне (ГРИБ) принимали участие школьники из различных регионов: не только из Москвы, но и, например, из Республики Коми, Пермского края.
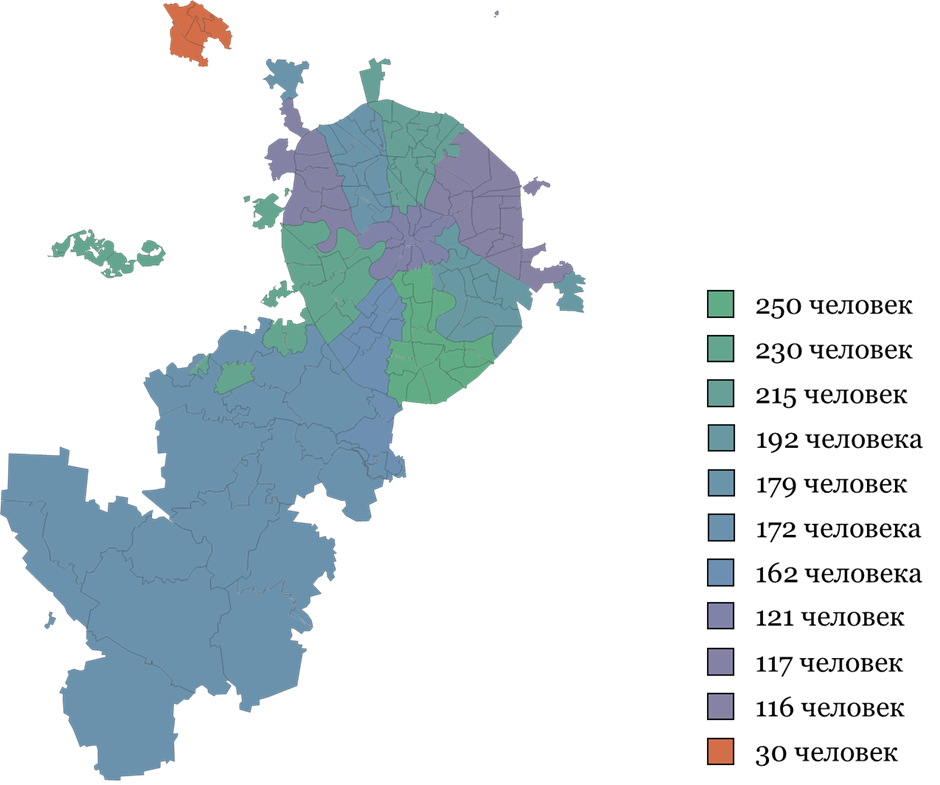
Всего в соревновании приняли участие более 2 000 участников, из них 1 784 человека — москвичи. Больше всего участников — из ЮАО (250 человек), ЗАО (230 человек), СВАО (215 человек.
Всего в соревновании участвовали обучающиеся из 152 московских школ. Наиболее представленными оказались школы № 1998 и 1430 (по 48 человек), школы № 1381 (46 обучающихся) и школа № 338 (45 человек). Список пятнадцати наиболее представленных на соревновании московских школ представлен ниже.
| Место | Образовательное учреждение | Делегация (чел.) |
| 1–2. | ГБОУ Школа № 1998 | 48 |
| ГБОУ Школа № 1430 | ||
| 3. | ГБОУ Школа № 1381 | 46 |
| 4. | ГБОУ Школа № 338 | 45 |
| 5. | ГБОУ Школа № 1392 им. Д.В. Рябинкина | 42 |
| 6–7. | ГБОУ Школа № 2121 | 36 |
| ГБОУ Школа № 1223 | 36 | |
| 8. | ГБОУ Школа № 2100 | 35 |
| 9. | ГБОУ Школа № 1636 | 31 |
| 10. | ГБОУ Школа Бибирево | 30 |
| 11. | ГБОУ Школа № 1101 | 29 |
| 12. | ГБОУ «Школа на Яузе» | 28 |
| 13. | ГБОУ «Московская международная школа» | 26 |
| 14–15. | ГБОУ Школа № 1434 | 25 |
| ГБОУ Школа № 2010 | 25 |
Что решали участники?
КОСМОС — это сюжетная игра: каждый сезон мы сочиняем новую фантастическую приключенческую повесть или постапокалиптическую дистопию, в которые попадают команды-экипажи.
Весной 2023 года участники перенеслись в 2323 год, где ничего не подозревающее человечество атаковано «выращенным» им же искусственным интеллектом «А-800», который захватывает сначала флагман орбитального флота «Астер», а затем, проникая все глубже в интернет, покоряет все сферы человеческой жизни. Участникам нужно подготовиться к апокалипсису, проверить убежища, подумать о том, как сохранить культурное и материальное наследие будущим поколениям… Но команда не замечает, как из-за разрушительного удара всей армадой космического флота под руководством «А-800» Земля отбрасывается на несколько веков назад. В финале участники стоят перед выходом из резервного люка: где они окажутся, выйдя из убежища?
В рамках этой истории командам было предложено решить 16 комплексных задач. Мы расскажем о самых сложных и самых креативных.
Для того чтобы определить условную сложность задач, нами были рассчитаны медианная удельная сложность dM и удельная сложность по среднему dA:
- для расчета первого показателя вычислялся результат средней команды по каждому заданию, определялся процент, который составил этот результат, который впоследствие вычитался из ста процентов — таким образом, это показатель, показывающий процентиль команд, продемонстрировавших результат хуже средней команды:
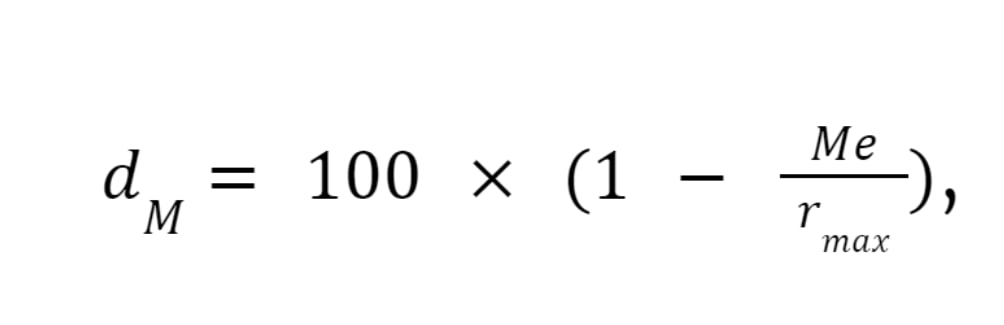
где Me — медиана, rmax — максимально возможный балл за задание;
- для расчета второго показателя из ста процентов вычислялся процент, который составило среднее по всем командам за каждую отдельную задачу — это значение следует интерпретировать как объем баллов по критериям, которые были недополучены участниками в среднем:
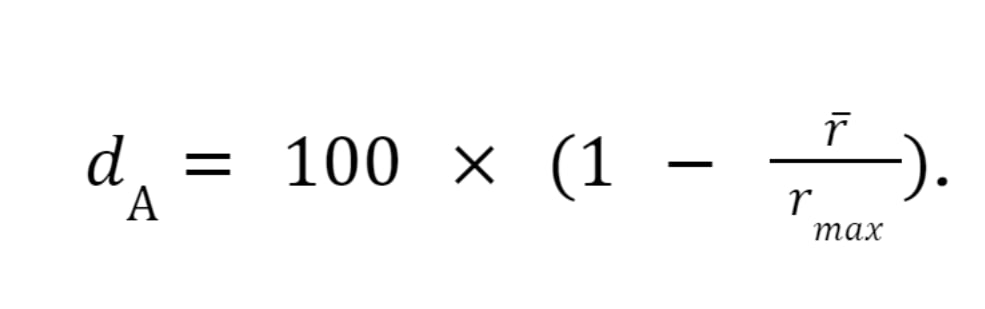
Важное замечание: объем реальных выборок небольшой (максимальное значение N = 74), он постоянно уменьшался в связи с тем, что после каждого этапа происходил новый отбор команд в следующий соревновательный этап.
Наиболее сложными в рамках весеннего сезона КОСМОСа 2023 года оказались
- задача № 2 первого соревновательного этапа по физике (dM = 90%, dA = 79,06%);
- задача № 3 того же этапа по астрономии (dM = 90%, dA = 88,3%);
- задача № 1 четвертого соревновательного этапа по биологии (dM = 82,35%, dA = 77,43%);
- задача № 1 пятого соревновательного этапа — финала — по лингвистике (русскому языку) (dM = 95%, dA = 95,79%).
Познакомимся с задачей по физике:
Ваша программа была принята адмирал-консулом. Пришло новое обращение: Центр баллистических сил сдерживания просит вас изучить технические характеристики новых ракет, разрабатываемых в секретной лаборатории, расположенной на поверхности Марса. В дальнейшем эти ракеты планируется поставить на вооружение «Астера».
Инженеры секретной лаборатории на Марсе проводят испытания новых ракет путем измерения дальности их полета. Ракету массой 1 т (500 кг из которых — топливо) закрепляют на неподвижном стенде под углом 45° к поверхности Марса. Двигатель ракеты включается дважды во время полета ракеты. После первого пуска двигателя сжигается ровно половина всего топлива. Второй запуск двигателя происходит в верхней точки траектории, при этом сжигается оставшаяся часть топлива. Считайте, что топливо в обоих запусках сжигается крайне быстро (временем сжигания можно пренебречь, скорость ракеты меняется скачком сразу после сжигания топлива). Ракета не оснащена никакими дополнительными стабилизирующими двигателями, так что импульс, который она получает в результате сжигания топлива, направлен строго по направлению скорости ракеты. Испытания показали, что дальность полета ракеты составила 10 км. Определите по этим данным скорость (относительно корпуса ракеты) истечения газов сгорающего топлива.
Сопротивлением атмосферы Марса и кривизной его поверхности можно пренебречь. Масса Марса составляет 0,107 земной массы, радиус — 0,532 земного, ускорение свободного падения на поверхности Земли считайте равным 9,8 м/с2.

Кирилл Львов, заведующий кафедрой физики ОРТШ Центра педагогического мастерства и автор данной задачи, отмечает:
«Такие задачи — авторские, с замысловатым, но жизненным условием, приближенным к реальным процессам и явлениям, требуют ещё одного навыка помимо банального применения физических законов и математических преобразований: такие задачи требуют анализа текста, выделения в нем физических «хвостиков», за которые нужно ухватиться и раскрутить физический клубок.
Нужно понять, осознать, какие процессы и каким образом они происходят, а после этого наложить на них математику. В данной задаче нужно было понять, что в момент старта работает закон сохранения импульса, который позволяет определить начальную скорость ракеты.
На первом участке полета движение ракеты является равноускоренным, и по известным формулам можно определить скорость ракеты в конце первого участка. Далее снова работает закон сохранения импульса, а затем — снова равноускоренное движение».
Следующая сложная задача — по астрономии из того же этапа:
Центральный космический хаб готовится к переводу линкора «Астер» в режим наблюдения. Отдел защитных разработок «Скайнет» планирует обучить искусственный интеллект «А-800» для того, чтобы он мог уничтожать угрожающие Земле объекты в автоматическом порядке с использованием оружия, расположенного на линкоре «Астер».
Управление по координации планетарной обороны США еще в далёком ХХ веке признала опасными для всей жизни на Земле астероиды размером больше 10 км. Выберите из данной таблицы астероиды, которые потенциально могут угрожать Земле.
Примечание: яркость астероидов удобнее всего сравнивать с Луной. Видимая звездная величина Луны составляет -12.7m, радиус Луны — 1740 км, а альбедо — 0,12. Необходимо считать, что поток падающего от Солнца света на Луну и астероиды одинаковый.
| № | Видимая звездная величина | Горизонтальный параллакс | Хим. состав | Альбедо | Большая полуось | Эксцентриситет | Сжатие астероида |
| 1. | -2m | 1,2’ | Fe, Si | 0,5 | 30 а.е. | 0,995 | 0 |
| 2. | -4m | 0,4’ | H20, Si | 0,45 | 45 а.е. | 0,97 | 0,2 |
| 3. | -7m | 0,3’ | H2O | 0,6 | 12 а.е. | 0,88 | 0 |
| 4. | -5m | 1,5’ | Mg, Au | 0,38 | 0,7 а.е. | 0,3 | 0,4 |
| 5. | -8m | 0,24’ | Au, Fe | 0,48 | 4 а.е. | 0,81 | 0,05 |
| 6. | -9m | 0,41’ | Fe, Si | 0,5 | 1,5 а.е. | 0,1 | 0,25 |
В качестве ответа укажите:
- Какие параметры имеют значение для изучения «Скайнетом»?
- Диаметр всех астероидов (не забудьте указать единицы измерения).
- Номера астероидов, которые потенциально опасны для Земли.

Мы попросили Алексея Лужнова, заведующего кафедрой астрономии ОРТШ Центра педагогического мастерства, а также автора приведенной задачи, прокомментировать это задание и дать рекомендации участникам:
«Во-первых, необходимо повторить законы Кеплера: приведенная задача была в основном на положение орбит. Участникам было необходимо установить, пересекутся орбиты небесных тел или нет. Второй важный совет — почитать про звёздные величины и освещённость: как последняя зависит от расстояния до тела и от его радиуса.
Задание, конечно, было сложным, но решаемым!«
Решение доступно для просмотра в этой публикации и на сайте в разделе «Материалы предыдущего сезона».
Перейдём к задаче по биологии из четвертого соревновательного этапа.
Для производства пищи в убежищах используются сложные системы сельского хозяйства, основанные на гидропонном выращивании культурных растений.
Для обеспечения максимальной автономности убежищ в подобных системах поддерживается искусственно созданный круговорот биогенов, в частности азота. Перед спуском в убежище у вас появилась возможность дистанционно проверить и протестировать состояние сельскохозяйственных систем…
Вопрос №1. Некоторые из отсеков, предназначенных для производства пищи, оказались выведены из строя! К счастью, в вашем распоряжении, есть показатели датчиков, замеряющих относительную концентрацию находящихся в среде азотсодержащих веществ. Определите, в каких отсеках наблюдаются проблемы с нормальной циркуляцией биогенов. Обоснуйте ваш выбор.
Вопрос №2. Для восстановления нормального круговорота биогенов вы решили внести изменения в бактериальные сообщества «проблемных» отсеков. Предложите, какие отсеки нуждаются в дополнительных «порциях» азотфиксирующих, нитрифицирующих или денитрифицирующих бактерий.
Вопрос №3. Каждый из отсеков также разделен на несколько «ферм» — изолированных искусственных экосистем. Для обеспечения полноценного рациона обитателей убежища (то есть производства не только растительной пищи) каждая «ферма» в идеале должна представлять собой простую пищевую цепочку из продуцентов, консументов первого порядка, консументов второго порядка и редуцентов.
При попытке проверить состояние «ферм» в оставшемся рабочем отсеке вы обнаружили, что из-за давнего сбоя на сервере данные о видовом составе «ферм» оказались утрачены; при этом, к счастью, сохранились данные об относительном количестве надземной биомассы.
Предположите (на основании этих данных), в какой из «ферм»: 1) присутствуют только продуценты; 2) присутствуют продуценты и консументы первого порядка; 3) присутствуют продуценты и консументы первого и второго порядка. Обоснуйте свой выбор.
Вопрос №4. Для стабилизации системы вы решили добавить в «ферму», содержащую все необходимые звенья пищевой цепочки, ещё один организм — хищника, питающегося консументами и первого, и второго порядка. Каким образом может измениться надземная биомасса «фермы» относительно исходной пищевой цепочки? Ответ обоснуйте.
Николай Мельников, методист кафедры биологии ОРТШ Центра педагогического мастерства, рекомендует:
«В биологии и экологии много внимания уделяют круговороту биогенных элементов в природе. Это важная и нужная тема для понимания современных тенденций в экологической обстановке, сельском хозяйстве, агротехнике и т.д. Важно понимать, в какой форме биогенные элементы могут усваиваться организмами и в какой могут быть для них вредны, равно как и представлять себе основные пути превращения этих форм. Вторая половина задачи посвящена биомассам, а где биомассы — там почти всегда присутствует правило Линдемана. Его надо всегда помнить и всегда применять вместе с знанием, как устроены пищевые цепочки — тогда решение задачи не представит особой проблемы».

Полное решение — здесь и на сайте.
Переходим к задаче с последнего — очного финального — этапа. Пожалуй, к самому сложному заданию всего весеннего сезона соревнования — к вопросу по лингвистике.
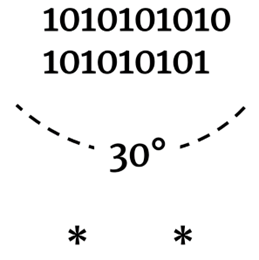
Отправившись на исследование надписей, вы обнаружили две группы граффити.
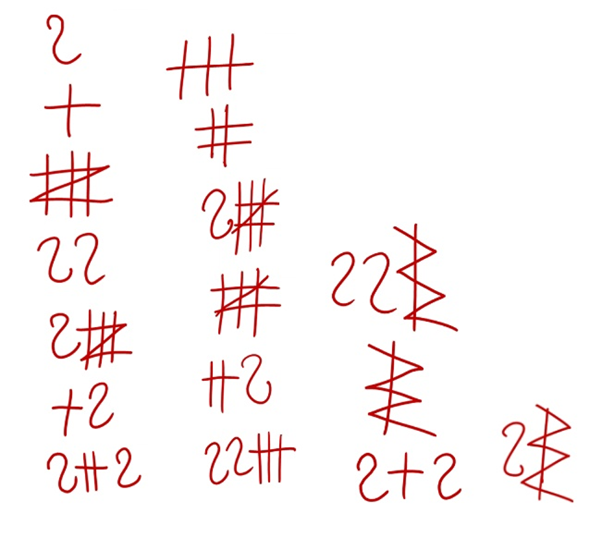
⠀⠀⠀⠀⠀
⠀⠀⠀⠀⠀

Предположив, что равенство количества элементов в каждой группе неслучайно, вы решаете установить соответствия между элементами из первой и второй групп.
Вопрос № 1. Что обозначается данными элементами?
Вопрос № 2. Установите соответствие между элементами в двух группах. Ответ аргументируйте.
Вы решаете пройти далее по укрытию. На каменной стене вы, как вам кажется, находите таблицу соответствий, где сколот некоторый фрагмент:
Вопрос № 3. Восстановите сколотый фрагмент. Ответ аргументируйте.
Вопрос № 4. Какой элемент типа первой группы будет соответствовать следующему элементу типа второй группы: ?
Варианты ответа:
| (а) | (б) | (в) | (г) |
Ответ аргументируйте.
Валерия Быкова, заведующая кафедрой русского языка ОРТШ Центра педагогического мастерства, член жюри пятого соревновательного этапа весеннего сезона КОСМОСа 2023 года, поделилась такими впечатлениями и рекомендациями:

«Участникам не хватило опыта в решении так называемых самодостаточных лингвистических задач, когда нужно долго и вдумчиво анализировать представленный материал без привлечения дополнительных фоновых знаний.
Кроме того, можно посоветовать отказаться от восприятия лингвистики как исключительно гуманитарной науки: мы тоже работаем с системами счисления, у нас тоже можно считать!»
Мы же — на правах автора задачи — поделимся решением задачи.
Обе группы символов обозначают числа, причём во второй группе элементов представлены числовые записи допетровской эпохи, когда по греческому образцу определённый объём букв мог представлять некоторое числовое значение: а — первая буква алфавита, например, обозначала один, а к — двадцать. Последнее изучают все олимпиадники, которые готовятся к соревнованиям по русскому языку. Тем не менее, найти соответствия между символами из разных групп можно без дополнительных знаний. Символы первой группы отражают двенадцатеричную систему счета, символ каждого разряда — изогнутая «змейка», положительные единицы располагаются справа от символа разряда: так, например, 17 — это 12+5; отрицательные единицы в количестве от 1 до 2 располагаются слева от символа разряда: так, например, 10 — это -2 + 12; количество точек пересечения линий на символах единиц равно числу, которые они обозначают.
| Установленные соответствия | |||
| Вторая группа | Первая группа | Вторая группа | Первая группа |
| а → | ꙁі → | ||
| г → | ѳі → | ||
| д → | ка → | ||
| є → | кв → | ||
| ꙁ → | кг → | ||
| ѳ → | кд → | ||
| i → | кꙁ → | ||
| аі → | кѳ → | ||
| ві → | |||
Переходим далее к вопросу про зайцев. Число дi — это четырнадцать, то есть двенадцать (символ разряда) и две положительные единицы справа; количество зайцев на рисунке также равно четырнадцати, значит, сколотый фрагмент выглядит так:
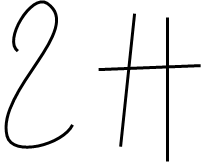
Наконец, вопрос № 4. Правильный ответ — (в), поскольку 20 — это 12+8, то есть записано должно быть как символ разряда и единицы справа, по количеству пересечений на символе единицы не подходит вариант (а), но подходит (в).
Хочется отметить, что задания не только сложные, но и творческие, интересные. «Победителями» в негласной номинации на самую методически неординарную задачу стали кафедры литературы и истории искусств (МХК) ОРТШ Центра педагогического мастерства.
Когда машины пытаются поработить человечество, первым делом они уничтожают культурный код. Вирус стёр все литературные тексты и упоминания о предметах искусства, заменив информацию о них на раскодированный набор знаков и изображений. Пока вы помните, вы можете восстановить исходный код.
Попробуйте понять логику машины: определите, о каких литературных произведениях и культурных объектах идёт речь. Для текстов укажите автора и название. Для предметов искусства — название, автора (если известен) и местоположение.
Помимо дешифровок участникам была предложена творческая часть.
Придумайте технологию, которая позволит защитить информацию о культурных ценностях человечества. Будет ли это двойное квантовое шифрование? Может, проще собрать всё в одно гигантское хранилище и обеспечить механическую защиту?
Опишите вашу концепцию в 7–10 предложениях. Проиллюстрируйте работу системы на примерах.
Турнир Московских Ынтеллектуальных Школьников запомнился участникам разнообразными задачами: кому-то понравились вопросы о животных, кому-то — о рыбах, а кому-то — о киберспорте.
Разумеется, все задачи были связаны с русским языком и лингвистикой!
Формат соревнования не предполагает ведение статистики, выделение наиболее сложных задач.
Тем не менее, преподаватели кафедры русского языка ОРТШ Центра педагогического мастерства подготовили ряд видеоразборов, которые могут быть полезны всем, кто хочет принять участие в МЫШе.
Для турнира было разработано 175 новых задач, которые, конечно, нельзя разобрать в рамках одного отчёта. Тем не менее, мы предлагаем вам решить ещё три загадки и проверить свои ответы!
1. Удвоенные буквы за 2000.
Диалог в гипермаркете бытовых товаров, общаются два человека на расстоянии:
— Сколько ленты!
— Да, Х! Как известно, в таких гипермаркетах торгуют и стройматериалами, и домашними растениями.
Если известно, что Х — это пароним фразы «Сколько ленты!«, установите его.
2. Старье за 1000.
Соберитесь с мыслями, последний вопрос в этой теме. Каково значение слова алабор? Подберите употребимое сейчас прилагательное, отрицающее значение корня. В ответе укажите искомое значение и отысканное прилагательное.
3. Расшифруйте ребус.
Для задач I ГРИБа, которых было шестнадцать — четыре в двух пригласительных турах и двенадцать в шести соревновательных — мы воспользовались той же методикой расчета dM и dA, как и в случае с КОСМОСом (при максимальном значении N = 284). Наиболее сложными стали:
- задачи по биологии в пятом и третьем соревновательных этапах (dM = 83,34%, dA = 80,42% и dM = 70%, dA = 61,98% соответственно);
- задачи по химии во втором и четвертом соревновательных этапах (dM = 70%, dA = 62,18% и dM = 68,74%, dA = 67,34% соответственно).
Наиболее трудное задание по биологии, по-видимому, оказалось не столько методически или академически сложным, сколько физически: по условиям задачи участникам было необходимо сдать закрашенные схемы.
У рыб нужно найти и закрасить мозговой череп, жаберные дуги, челюсти, жаберные щели. Их эволюционно можно обнаружить и у человека.
Задание по биологии из третьего соревновательного этапа (второе по сложности из указанных) предполагало работу со схемами замещения эпидермиса у паразитических плоских червей.
Участникам было необходимо разработать лекарство для крупного рогатого скота, цель которого — уничтожение межклеточных контактов эпидермиса червя. Наиболее сложным вопросом в рамках этого задания был следующий:
«На какую стадию жизненного цикла сосальщика будет действовать это лекарство?»
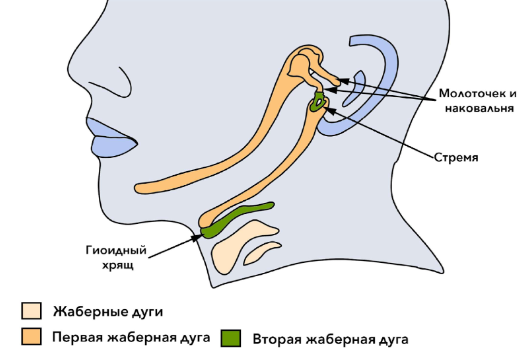
По-видимому, ответ мирацидий является достаточно сложным термином, на который будущим участникам ГРИБа следует обратить внимание.
Мы также подготовили несколько видеоразборов интересных задач из прошедшего соревнования, в котором авторы и члены жюри рассматривают наиболее сложные вопросы.
Интересный факт! Наиболее популярное название команды на весеннем ГРИБе — «Хламидомонада». Команд с таким наименованием было целых три: из ГБОУ Школа № 1586, ГБОУ Школа № 1015, а также из Московской международной школы. Помимо этого, в соревновании участвовали «Хламидомонады« из ГБОУ Школа № 1416 «Лианозово».
Как устроены УТЧ изнутри?
В команде учебно-тренировочных чемпионатов ЦПМ весной было семь человек:
- Денис Карелин
менеджер службы поддержки - Анастасия Сумеди
дизайнер - Анастасия Кондратьева
руководитель веб-разработки - Анна Карпова
менеджер по обеспечению - Анастасия Волкова
главный организатор - Анжелика Загашвили
аналитик обратной связи - А также ваш покорный слуга Роман Илюшин
Ежедневно мы обрабатывали не менее двенадцати звонков и девятнадцати писем, эти объёмы в дни проведения этапов увеличивались четверократно! В соревнованиях было задействовано более тридцати образовательных организаций города Москвы, которые предоставили свои площадки. Наиболее часто мы проводили УТЧ на площадках следуюших школ (по три раза на каждой):
ГБОУ Школа № 338 имени Героя Советского Союза А. Ф. Авдеева
ГБОУ Школа № 56 имени академика В. А. Легасова
ГБОУ Школа № 2090 имени Героя Советского Союза Л. Х. Паперника
ГБОУ Школа № 1440
Мы благодарим педагогов и администрацию этих школ, которые участвовали в организации и проведении соревнований.
Осенью Центр педагогического мастерства проводит новый сезон учебно-тренировочных чемпионатов: помимо КОСМОСа, ГРИБа и VIII турнира МЫШ, пройдут КУСТ (Командный ученический страноведческий турнир) и ТИТАН (IT-турнир по STEM-наукам)! Регистрация доступна на сайте турнир.цпм.рф.